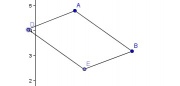
Parallélogramme
Sommaire
Propriétés
Caractéristiques
Si un quadrilatère est un parallélogramme alors :
- ses côtés opposés sont de même longueur
- ses côtés opposés sont parallèles
- ses angles opposés sont de même mesure
- ses angles consécutifs sont supplémentaires
- ses diagonales se coupent en leur milieu
- il admet un centre de symétrie : le point d'intersection de ses diagonales
Reconaissance d'un parallélogramme
- Si un quadrilatère (non croisé) a ses côtés opposés parallèles, alors c'est un parallélogramme.
- Si un quadrilatère (non croisé) a ses côtés opposés de même longueur, alors c'est un parallélogramme.
- Si un quadrilatère (non croisé) a une paire de côtés opposés parallèles et de même longueur alors ce quadrilatère est un parallélogramme.
- Si les diagonales d'un quadrilatère se coupent en leur milieu, alors c'est un parallélogramme.
- Si les angles opposés d'un quadrilatère sont de même mesure, alors c'est un parallélogramme.
- Si un quadrilatère admet un centre de symétrie, alors c'est un parallélogramme.
Parallélogrammes particuliers
Le rectangle, le losange et le carré sont des parallélogrammes particuliers : c'est-à-dire qu'ils réunissent toutes les propriétés du parallélogramme ordinaire, mais ils se distinguent de celui-ci par d'autres propriétés.
Aire et périmètre d'un parallélogramme
L'aire d'un parallélogramme se calcule à l'aide de cette unique formule :Le périmètre d'un parallélogramme est très simple à calculer ; il suffit de calculer la somme des longueurs de ses quatre côtés.






 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels