Droite remarquable

Les droites remarquables d'un triangle sont des droites qui possèdent des propriétés remarquables, autrement dit des caractéristiques particulières.

D'un point de vue géométrique, ces droites sont donc intéressantes à observer.

Dans le cas d'un triangle équilatéral, les droites remarquables sont confondues.

Les médiatrices

Qu'est ce qu'une médiatrice ?

La médiatrice d'un segment est la droite perpendiculaire à ce segment et passant par son milieu.

> Voir l'article détaillé : Médiatrice

Les médiatrices dans le triangle

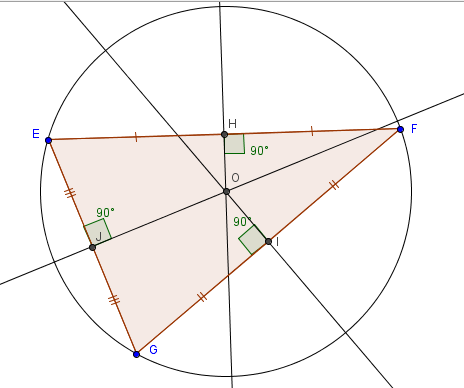
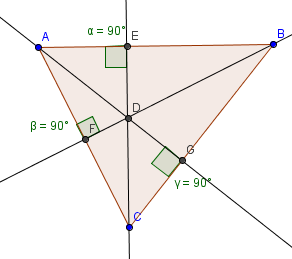
EFG est un triangle quelconque. Les 3 médiatrices d'un triangle sont concourantes (c'est-à-dire que les 3 droites se croisent en un point).

O est le point d'intersection des 3 médiatrices et est le centre du cercle circonscrit (c'est-à-dire le cercle passant par les 3 sommets du triangle).

Comme les points appartenant au cercle sont tous à la même distance du centre alors EO=FO=GO.

Conclusion

Le point d’intersection des 3 médiatrices d'un triangle donne le centre du cercle qui passe par les 3 sommets du triangle : le cercle circonscrit.

Les médianes

Définition :
Dans un triangle, la médiane issue d’un sommet passe par ce sommet et par le milieu du côté opposé.

Les médianes dans un triangle :

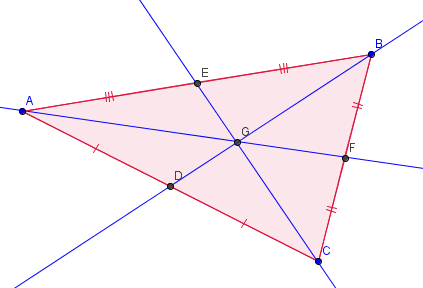
ABC est un triangle quelconque. Les 3 médianes d’un triangle sont concourantes (=c’est-à-dire que les 3 droites se coupent en un point).
G est le point d’intersection des 3 droites. C’est le centre de gravité du triangle, il se trouve aux deux tiers du segment médiane en partant du sommet.
Le centre de gravité est le seul point du triangle permettant de le faire tenir en équilibre. Le segment médiane partage le triangle en deux parties de même aire.
Conclusion :
Dans un triangle, l’intersection des médianes donne le centre de gravité.

Les hauteurs

Définition :
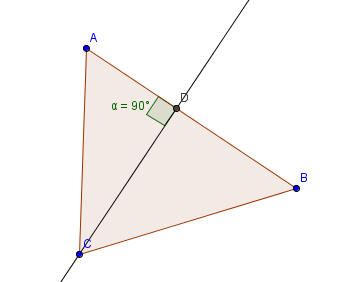
Dans un triangle, la hauteur issue d’un sommet passe par ce sommet et est perpendiculaire au côté opposé.

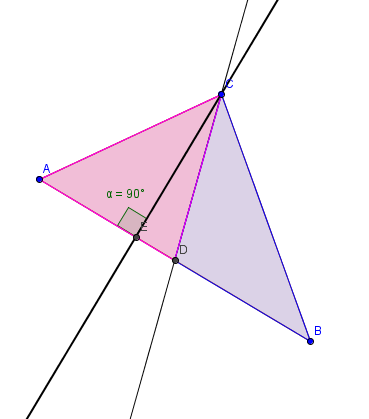
Les hauteurs dans un triangle :
Dans un triangle, les trois hauteurs sont concourantes. Leur point d’intersection forme l’orthocentre du triangle.
Conclusion :
L’orthocentre est formé par les hauteurs.

Les bissectrices

Définition :
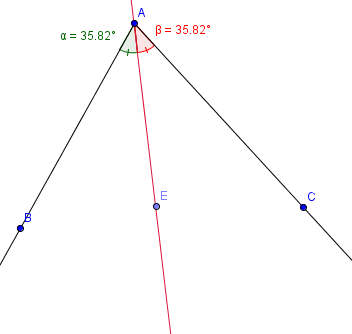
La bissectrice est la droite qui coupe l’angle en deux parties égales.

Les bissectrices dans un triangle :
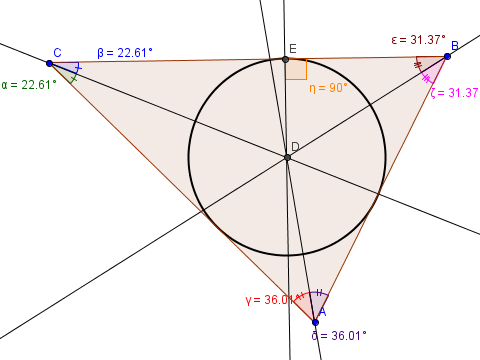
Dans un triangle, les bissectrices sont concourantes. Leur point d’intersection forme le centre du cercle inscrit. Le cercle inscrit est tangent aux trois côtés du triangle.
La tangente à un cercle (C) en un point A est la droite perpendiculaire au rayon du cercle issue de A passant par A.
Conclusion :
Le centre du cercle inscrit est formé par les bissectrices.

Les cas particuliers :

Triangle rectangle :
Dans un triangle rectangle, le point d’intersection des trois médiatrices (le centre du cercle circonscrit) et le milieu de l’hypoténuse (le côté le plus long) sont confondus.

Triangle isocèle :
Dans un triangle isocèle, la médiatrice, la hauteur, la médiane et la bissectrice sont confondues. Alors le centre du cercle circonscrit, l’orthocentre, le centre de gravité et le centre de cercle inscrit appartiennent à cette droite.

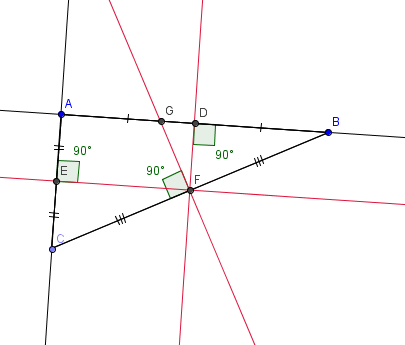
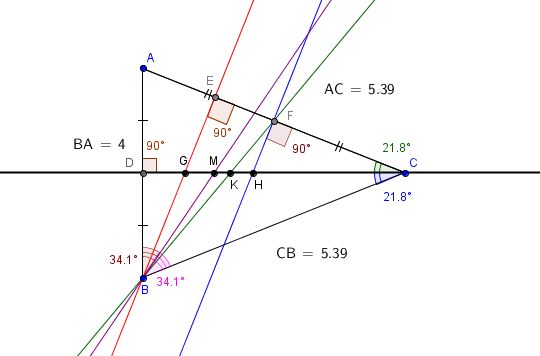
Explication de la figure :
ABC est un triangle isocèle en C, où F et D sont les milieux respectifs de [AC] et [AB].
Les médiatrices (FH) et (DC) se coupent en H. Donc le point H est le centre du cercle circonscrit.
Les deux hauteurs (EB) et (DC) se coupent en G. Donc le point G est l’orthocentre.
Les deux médianes (DC) et (FB) se coupent en K. Donc K est le centre de gravité.
Les deux bissectrices (DC) et (MB) se coupent en M. Donc M est le centre du cercle inscrit.
Conclusion : (DC) est à la fois une médiatrice, une hauteur, une bissectrice et une médiane.

Triangle équilatéral :
Dans un triangle équilatéral toutes les bissectrices, les médiatrices, les hauteurs et les médianes sont confondues. Leur (seul) point d’intersection est à la fois le centre du cercle circonscrit, le centre du cercle inscrit, l’orthocentre et le centre de gravité.