Agrandissement et réduction (mathématiques)

Dans un agrandissement ou une réduction, toutes les longueurs sont proportionnelles à celles de la figure initiale.

Le coefficient de proportionnalité s'appelle le taux d'agrandissement (ou de réduction) [ou rapport].

Les deux figures ont la même forme, il y a conservation des angles, de la perpendicularité et du parallélisme.

Si la figure F est l'agrandissement de la figure F' de coefficient k, alors F' est la réduction de F de coefficient k.

Exemple :

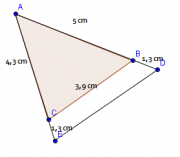
AB = 5 cm; AC = 4,3 cm et BC = 3,9 cm
Le triangle ADE est un agrandissement de rapport 1,3 du triangle ABC de la figure ci-dessous tel que D appartienne à [AB) et E appartienne à [AC)
Calcule les longueurs des côtés du triangle ADE.

Comme ADE est un agrandissement de ABC, de rapport 1,3, alors:
AD = 1,3 x AB = 1,3 x 5 = 6,5 cm
AE = 1,3 x AC = 1,3 x 4,3 = 5,59 cm
ED = 1,3 x ED = 1,3 x 3,9= 5,07 cm